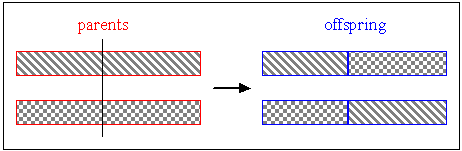
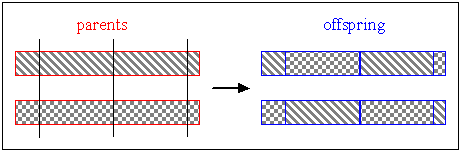
Typical Variation Operators in cEA
The first step in a cEA generation is fitness assignment,
which is done simultaneously for all individuals. This fitness assignment process
consists on selecting a value to each individual according to its proximity
to the problem solution.
After this first step the three next genetic operators take
place locally within a small neighborhood:
- Selection:
With this operator the individuals producing offspring are chosen.
- Reproduction:
This step allows us to generate the offspring from the parents chosen in selection
step.
- Replacement:
This last operator is applied for including into the population the new individuals
generated in reproduction step without increasing the population size.
Selection
Selection is a process in which fitter individuals are selected
to reproduce offspring for the next generation. In nature, an individual undergo
two different selection pressures before producing its offspring, i.e., survival
to adult state and find of its mates. Selection of EAs models these processes.
Some "luck" (random effect) is usually involved too. The selection
process is the step that guides the evolutionary algorithm towards ever-better
solutions.
We will expose some different selection schemes. We focus
on cEAs with a single topology, the frequently used two
dimensional torus. A typical example would be a N
x N grid in which a single individual exists at each grid point
and interacts with its neighbors on nearby grid points.
As we are studying just the case of cellular EAs, all the
selection methods following are variants of Local selection
[Wrigh69]
wherein every individual resides inside a constrained environment called the
local neighborhood. Individuals interact only
with individuals inside this region. The selection methods used in cEAs are
typically the same that those used in panmistic EAs. The neighborhood is defined
by the structure in which the population is distributed. It can be seen as the
group of potential mating partners. The main selection methods used in the literature
are:
- Linear Rank Selection
[GB89]: the
neighborhood is sorted
according to the objective values. The selection of an individual depends
only on its position in the individuals rank and not on the actual objective
value.
The linear rank selection algorithm defines the target
sampling rate (TSR) of an individual x as:
TSR(x)
= Min + (Max - Min) rank(x)/(N - 1) |
(1) |
where rank(x) is the index
of x when the population is sorted in increasing
order based on fitness, and N is the population
size. Also, we impose the constraints that 0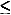 
TSR(x) , 
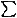TSR(x)
= N, 1
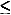Max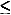
2, and Min + Max = 2.
The TSR is the number of times an individual should be
chosen as a parent for every N sampling operations.
- Roulette Wheel Selection:
This is the simplest selection scheme, also called stochastic sampling with
replacement [Gold89].
This is a stochastic algorithm and involves the following technique:
The individuals are mapped to contiguous segments of
a line, such that each individual's segment is equal in size to its fitness.
A random number is generated and the individual whose segment spans the
random number is selected. The process is repeated until the desired number
of individuals is obtained (called mating population). This technique is
analogous to a roulette wheel with each slice proportional in size to the
fitness.
In Figure 1 we can see a graphic example with the individuals
of Table 1, which shows the selection probability for 11 individuals, linear
ranking and selective pressure of 2 together with the fitness value. Individual
1 is the most fit individual and occupies the largest interval, whereas
individual 10 as the second least fit individual has the smallest interval
on the line (see figure 1). Individual 11, the least fit interval, has a
fitness value of 0 and get no chance for reproduction.
| Number of individual |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| fitness value |
2.0 |
1.8 |
1.6 |
1.4 |
1.2 |
1.0 |
0.8 |
0.6 |
0.4 |
0.2 |
0.0 |
| selection probability |
0.18 |
0.16 |
0.15 |
0.13 |
0.11 |
0.09 |
0.07 |
0.06 |
0.03 |
0.02 |
0.0 |
|
| Table 1. Selection probability and
fitness value |
 |
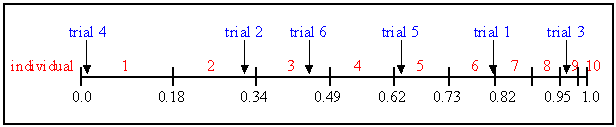| Figure 1. Roulette-wheel selection |
For selecting the mating population the appropriate number
of uniformly distributed random numbers (uniform distributed between 0.0
and 1.0) is independently generated. In Figure 1 we can see the selection
process of the individuals for the example in Table 1 for the sample of
these 6 random numbers: 0.81, 0.32, 0.96, 0.01, 0.65, 0.42.
The roulette-wheel selection algorithm provides a zero
bias but does not guarantee minimum spread.
- Stochastic Universal Sampling
[Bak87]:
This method provides zero bias and minimum
spread. The individuals are mapped to contiguous segments of a line, such
that each individual's segment is equal in size to its fitness exactly as
in roulette-wheel selection. Here equally spaced pointers are placed over
the line as many as there are individuals to be selected. Consider NPointer
the number of individuals to be selected, then the distance between the pointers
are 1/NPointer and
the position of the first pointer is given by a randomly generated number
in the range [0, 1/NPointer].
For 6 individuals to be selected, the distance between
the pointers is 1/6=0.167. Figure 2 shows the
selection for the sample of the random number 0.1 in the range [0, 0.167].
 |
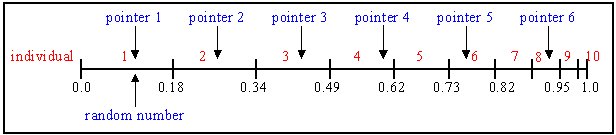| Figure 2. Stochastic universal sampling |
After selection the mating population
consists of the individuals: 1, 2, 3, 4, 6, 8.
Stochastic universal sampling ensures a selection of offspring which is
closer to what is deserved then roulette wheel selection.
- Truncation selection
[CK70]: Compared
to the previous methods modeling natural selection truncation is an artificial
selection method. It is used by breeders for large populations/mass selection.
In truncation selection individuals are sorted according
to their fitness. Only the best individuals are selected for parents. These
selected parents produce uniform at random offspring. The parameter for
truncation selection is the truncation threshold Trunc.
Trunc indicates the proportion of the population
to be selected as parents and takes values ranging from 50%-10%. Individuals
below the truncation threshold do not produce offspring.
-
Tournament selection
[GD91]: In
tournament selection [GD91]
a number Tour of
individuals is chosen randomly from the neighborhood
and the best individual from this group is selected as parent. This process
is repeated as often as individuals to choose. These selected parents produce
uniform at random offspring. The parameter for tournament selection is the
tournament size Tour.
Tour takes values
ranging from 2 - Nind
(number of individuals in neighborhood).
Reproduction
Reproduction is the mechanism that allows us to obtain offspring's
from one (asexual) or more (sexual) parents. Among reproduction operators the
following stand out:
Replacement
Replacement schemes are used by genetic algorithms with overlapping
populations to determine how the new individuals will be assimilated into the
population. Replace-worst and replace most-similar are the only really useful
replacement schemes. Sometimes replace-parent can be effective, but usually
when the parents are similar to the offspring, and this is just replace-most-similar.
- Replace if better: The offspring
replaces the studied individual only if its fitness value is greater.
- Replace always: The offspring
replaces the studied individual always.
- Replace worst: The offspring
replaces the worst individual of the neighborhood.
- Replace
best: The offspring replaces the best individual of the neighborhood.
- Replace random: The offspring
replaces an individual of the neighborhood selected randomly.
- Replace parent: The offspring
replaces one of its parents.
- Replace most similar (crowding):
The offspring replaces the individual of the neighborhood with closest chromosome
information.
Depending on when the replacement policy is applied we can
stand out two different kinds of cEA:
