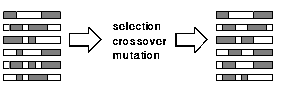
Synchronous and Asynchronous cEA
We can make a classification in sequential cEAs depending on if the whole population is actualized by the new one at the same time or not. The cEA of the first case are called synchronous, while those belonging to the later case are asynchronous.
In generational or synchronous cEA, the whole old population is replaced simultaneously by the offspring population at the end of each generation. We can achieve this by computing the full new generation incrementally onto a temporary population, and then replace the full old population with the new one. In Figure 1 we can see how does synchronous cEA work:
 |
| Figure 1. Synchronous cEA |
In the case of asynchronous algorithms, the individuals of the population are replaced by theirs offspring sequentially during the generation. So in this asynchronous cEAs we do not have to wait all the individuals to reproduce for replacing the old individuals of the population with the new ones. This way, one individual can match with the offspring of his neighbors to reproduce (see Figure 2).
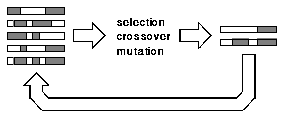 |
| Figure 2. Asynchronous cEA |
There are many ways for sequentially updating the cells of a cEA with a population on a 2D grid [SR99]. Here we will consider the following [AGTR02]:
A time step must be defined
to be the action of updating n times, which corresponds
to updating all the n
cells in the grid for LS, FRS and NRS, and possibly
less than n different cells in the uniform choice
method, since some cells might
be updated more than once. It should be noted that, with the exception of
fixed line sweep, the other asynchronous updating policies are non-deterministic,
representing an additional source of non-determinism besides that of the genetic
operators. An asynchronous parallel implementation could be easily derived for
these algorithms.
Synchronous vs. asynchronous
In Figure 1 we display the mean number of evaluations needed for all the algorithms described above to solve three different problems: a multimodal and deceptive (MMDP), a highly epistatic (P-PEAKS), and an irregular with continuous optimization (FMS) one [AGTR02].
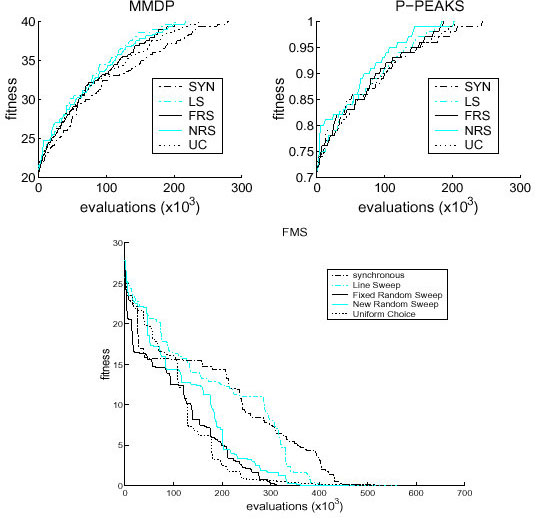 |
| Figure 3. A sample run of each update method for the MMDP, P-PEAKS, and for the FMS problem. |
In Figure 4 we display a graph of the evolution of the diversity (Entropy) for MMTP and P-PEAKS problems [AGTR02].
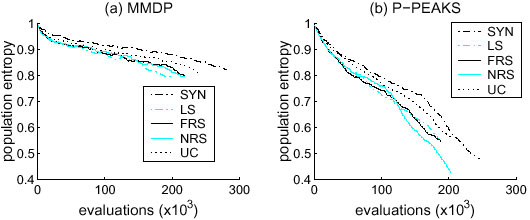 |
| Figure 4. A sample curve of the entropy of each update method for the MMDP (a) and for the P-PEAKS problem (b). |
Alba et al. concluded in [AGTR02] that, for any size of the search grid, the synchronous update policy is the best in terms of percentage of hits, because it always provides an equal or larger success rate with respect to any of the asynchronous policies.
However, considering the number of evaluations needed to locate the optimum (efficiency) the opposite conclusion is obtained: asynchronous methods are faster (sometimes much faster) than the synchronous one. A simple asynchronous policy such that Line Sweep (LS) provides the faster convergence for two of the problems (MMDP and P-PEAKS), while it shows a high and desirable success rate (similar to that of the synchronous update). In the hard FMS problem, Fixed Random Sweep got a considerably faster solution, and can be pointed out as a good approach.
Globally stated, fast convergence means local optima in evolutionary algorithms, but cellular EA’s in general, and the Line Sweep policy in particular, offers a good tradeoff solution to this problem without bothering researchers with a large number of parameters to be tuned (maybe only the ratio between the size of the grid and the neighborhood being used [AT00]).