Parallelizing cGAs

In the following points we will discuss some parallel cGAs designed for working in massively parallel computers. In these algorithms, each processing element processes a single individual:

• ASPARAGOS was introduced by Gorges-Schleuter [Gorg89a, Gorg89b] and Mühlenbein [Mühl89a, Mühl89b]. ASPARAGOS used a population structure that resembles a ladder with the upper and lower ends tied together. ASPARAGOS was used to solve some difficult combinatorial optimization problems with great success. Later, a linear population structure was used [Gorg91], and different mating strategies were compared [Gorg92].
  ASPARAGOS uses a local hillclimbing algorithm to improve the fitness of the individuals in its population. This makes it difficult to isolate the contribution of the spatial structure of the population to the search quality. However, all the empirical results show that ASPARAGOS is a very effective optimization tool.

• Manderick and Spiessens [MS89] implemented a fine-grained parallel GA with the population distributed on a 2-D grid. Selection and mating were only possible within a neighborhood, and the authors observed that the performance of the algorithm degraded as the size of the neighborhood increased. On the extreme, if the size of the neighborhood was big enough, this parallel GA was equivalent to a single panmistic population. 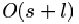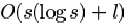The authors analyzed this algorithm theoretically in subsequent years [SM90, SM91], and their analysis showed that for a deme size s and a string length l, the time complexity of the algorithm was or time steps, depending on the selection scheme used.

• Schwehm [Schw92] [Schw94] compared the effect of using different structures on the population of fine-grained GAs. In these papers, a graph partitioning problem was used as a benchmark to test different population structures simulated on a MasPar MP-1 computer. Among the structures tested there were a ring, a torus, a 16 x 8 x 8 cube a 4 x 4 x 4 x 4 x 4 hypercube, and a 10-D binary hypercube. The algorithm with the torus structure converged faster than the other algorithms. The implementation of the algorithm is discussed in [Schw93].

• Thompson et al. developed in [TBK96] a massively parallel genetic algorithm for image analysis (MPGAIA) which run in a DAP 510 machine. This algorithm is similar to that of Manderick and Spiessens [MS89]. The main difference is the inclusion of real valued genes instead of grey coded binary genes of the model of Manderick and Spiessens.

• Shapiro and Naveta [SN94] used a fine-grained GA algorithm to predict the secondary structure of RNA. They used the native X-Net topology of the MasPar-2 computer to define the neighborhood of each individual. The X-Net topology connects a processing element to eight other processors. Different logical topologies were tested with the GA: all eight nearest neighbors, four nearest neighbors, and all neighbors within a specified distance d. The results for d>2 were the poorest, and the four-neighbor scheme consistently outperformed the topology with eight neighbors.

• Kohlmorgen et al. studied in [KSH96] the island and some variants of the neighborhood model on the massively parallel computer MasPar MP1 with 16K processors.