Measuring the Behavior of a cEA
We will introduce here some statistical measures that will be of especial interest for analyzing the mode of operation of cellular evolutionary algorithms. These statistical measures are both at genotypic (individuals) and phenotypic (population) levels. This study is taken from [CTTS98]. Refer to it for more complete information.
Basic Definitions and Notation
We can define the population as a vector of n
genotypes (individuals) ![]() .
The space of all possible populations is
.
The space of all possible populations is ![]() ,
where
,
where ![]() is the space of genotypes
is the space of genotypes ![]() (so
(so
![]() ).
The fitness of an individual will be
).
The fitness of an individual will be ![]() .
.
We can define an occupancy function ![]() such that , for all
such that , for all ![]() ,
,
![]() is the number of individuals in x sharing the same
genotype
is the number of individuals in x sharing the same
genotype ![]() ,
i.e., the occupancy number of
,
i.e., the occupancy number of ![]() in x. The size of population x,
in x. The size of population x,
![]() ,
is defined as
,
is defined as ![]() .
.
After that, we can now define a share function ![]() giving the fraction
giving the fraction ![]() of individuals in x that have genotype
of individuals in x that have genotype ![]() ,i.e.,
,i.e.,
![]() .
.
Consider the probability space ![]() ,
where
,
where ![]() is the algebra of the parts of
is the algebra of the parts of ![]() and
and![]() is
any probability measure on
is
any probability measure on ![]() .
Let us denote by
.
Let us denote by ![]() the probability of generating a population
the probability of generating a population ![]() by extracting n genotypes from
by extracting n genotypes from ![]() according to measure
according to measure![]() .
It can be shown that it is sufficient to know either of the two measures -
.
It can be shown that it is sufficient to know either of the two measures -![]() (over
the genotypes) or
(over
the genotypes) or ![]() (over the populations)- in order to reconstruct the other.
(over the populations)- in order to reconstruct the other.
The fitness function establishes a morphism from genotypes
into real numbers. If genotypes are distributed over ![]() according to a given probability measure
according to a given probability measure ![]() ,
then their fitness will be distributed over the real numbers according to a
probability measure
,
then their fitness will be distributed over the real numbers according to a
probability measure ![]() obtained from
obtained from![]() by
applying the same morphism:
by
applying the same morphism:
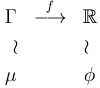 |
(1) |
The probability ![]() of a given fitness value
of a given fitness value ![]() is defined as the probability that an individual extracted from
is defined as the probability that an individual extracted from ![]() according to measure
according to measure ![]() has fitness
has fitness ![]() (or, if we think of fitness values as a continuous space, the probability density
of fitness
(or, if we think of fitness values as a continuous space, the probability density
of fitness ![]() ):
for all
):
for all ![]() ,
,
![]() where
where ![]() .
.
An EA can be regarded as a time-discrete stochastic process
| (2) |
having the probability space![]() as its base space,
as its base space, ![]() as its state space, and the natural numbers as the set of times, here called
generations.
as its state space, and the natural numbers as the set of times, here called
generations. ![]() must be thought of as the set of all the evolutionary trajectories,
must be thought of as the set of all the evolutionary trajectories, ![]() is a
is a ![]() -algebra
on
-algebra
on ![]() ,
and
,
and ![]() is a probability measure over
is a probability measure over ![]() .
.
The transition function of the evolutionary process, in turn based on the definition of the genetic operators, defines a sequence of probability measures over the generations.
Let ![]() denote the probability measure on the state space at time t;
for all populations
denote the probability measure on the state space at time t;
for all populations ![]() ,
,
| (3) |
In the same way, let ![]() denote the probability measure on space
denote the probability measure on space ![]() at time t; for all
at time t; for all ![]() ,
,
| (4) |
Similarly, we define the sequence of probability
functions ![]() as follows: for all
as follows: for all ![]() and
and ![]() ,
,
| (5) |
This class of statistics is based in some diversity indices at individuals level -genotypic-. Following we will see come functions which are significant of the population evolution at a genotypic level.
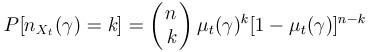 |
(6) |
thus,
and
. The share function
is perhaps more interesting, because it is an estimator of the probability measure
; its mean and variance can be calculated from those of
, yielding
and
(7)
The frequency of transitions
![]() of a population x of n
individuals (cells) is defined as the number of borders between homogeneous
blocks of cells having the same genotype, divided by the number of distinct
couples of adjacent cells. Another way of putting it is that
of a population x of n
individuals (cells) is defined as the number of borders between homogeneous
blocks of cells having the same genotype, divided by the number of distinct
couples of adjacent cells. Another way of putting it is that ![]() is the probability that two adjacent individuals (cells) have different
genotypes, i.e., belong to two different blocks.
is the probability that two adjacent individuals (cells) have different
genotypes, i.e., belong to two different blocks.
Formally, the frequency of transitions ![]() for a one-dimensional grid structure can be expressed as
for a one-dimensional grid structure can be expressed as
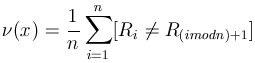 , , |
(8) |
where [![]() ]
denotes the indicator function of proposition
]
denotes the indicator function of proposition ![]() .
.
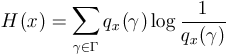 . . |
(9) |
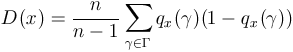 . . |
(10) |
Associated with a population x
of individuals, there is a fitness distribution. We will denote by ![]() its (discrete) probability function.
its (discrete) probability function.
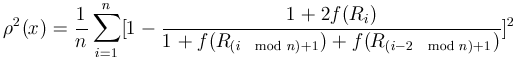 . . |
(11) |