The Generalized Rastrigin Function

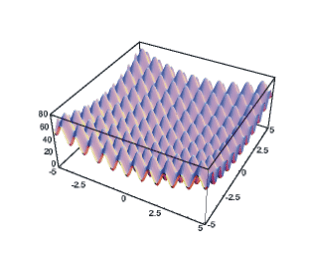
Description:

      The Generalized Rastrigin Function (Equation 1) is a typical example of non-linear multimodal function. It was first proposed by Rastrigin [TZ89] as a 2-dimensional function and has been generalized by Mühlenbein et al in [MSB91]. This function is a fairly difficult problem due to its large search space and its large number of local minima.

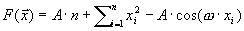                      (1)
        ; ;

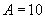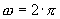      The Rastrigin function has a complexity of O(nln(n)), where n is the dimension of the problem. The surface of the function is determined by the external variables A and 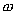, which control the amplitude and frequency modulation respectively.

Click here to get this description in tex format and here to get the figure in eps format.

Instances and best known solutions for those instances:

      In order to define an instance of this function we need to provide the dimension of the problem (n). The optimum solution of the problem is the vector v = (0,...,0) with F(v) = 0.

Related Papers:

[TZ89] A. Törn and A. Zilinskas. "Global Optimization". Lecture Notes in Computer Science, Nº 350, Springer-Verlag, Berlin,1989.

[MSB91] H. Mühlenbein, D. Schomisch and J. Born. "The Parallel Genetic Algorithm as Function Optimizer ". Parallel Computing, 17, pages 619-632,1991.

Click here to get the bibliography in bibtex fotmat.