The Quadratic Assignment Problem

Description:

The Quadratic Assignment Problem is a classified NP-hard optimization problem. It can be defined as:

Input:
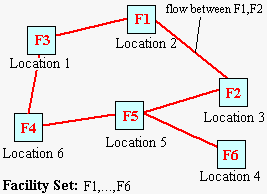
-A set of facilities F={f₁,...,f_n}.
-A set of locations D={d₁,...,d_n}.
-Material flow Flow(i,j) between pairs of facilities f_i,f_j.
-Distance Dist(i,j) between pairs of locations d_i,d_j.

Output:
-Assignment A defined as:

Statement of the Problem

In a standard QAP problem in location theory, we are given n facilities which are to be located in n locations. It has been defined a 'material' flow between pairs of facilities and a distance between the locations. To measure the cost of each possible assignment (there are n! of them) we multiply the prescribed flow between each pair of facilities by the distance between their assigned locations, and sum over all the pairs. The objective is to minimize the overall cost C of the layout.

Although, not required by the formulation, we will restrict our discussion to problems in which the flow matrix is symetric, i.e., the flow from facility i to j is the same as the flow from j to i.

Problem Instances

In order to define an instance of this problem we need to provide the full list of facilities and available locations. We also have to prescribe the flow between each pair of facilities and the distance between the locations of the instace.

Related Bibliography and Papers