The Polynomial Fitting Problem
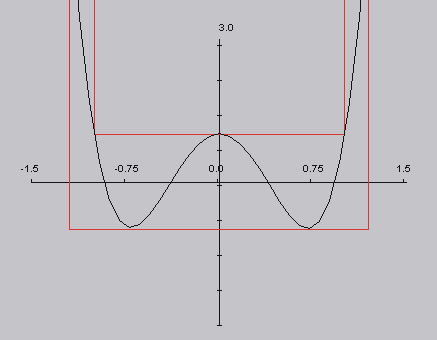
Description:
The Polynomial
Fitting Problem has its roots in electronic filter design [RG75],
and challenges an optimization procedure by forcing it to find parameter
values with grossly different magnitudes, something very common in technical
systems. The first metaheuristic used to deal with this problem has been
presented in [SP95] . The problem lies in finding
the coefficients of the following polynomial in 
:
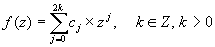
such that
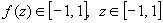and
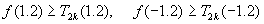
where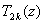 
is a Chebychev polynomial of degree 
.
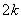The Chebychev Polynomials are defined recursively according to the difference
equation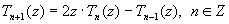 
and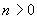 
,
with the initial conditions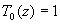 
and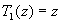 
.
The solution to the Polynomial Fitting Problem consists
of the coefficients of .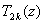
This polynomial oscillates between -1 and 1 when its argument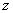
is between -1 and 1. Outside this region, the polynomial rises steeply
in the direction of high positive ordinate values.
If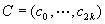 
is
a solution and
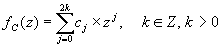
then the pseudocode algorithm shown below is used in
order to transform the constraints of this problem into an objective function
to be minimized, called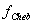 
[HL00,ALN03]. Each parameter
of this function (coefficient of the polynomial to fit to) is in the range
.
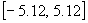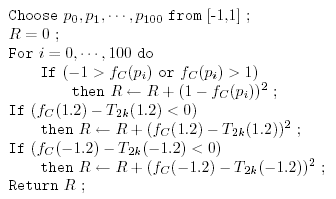
Click here to get this description in tex format and here to get the figure in eps format.
Instances and best known solutions for those instances:
The instances of this problem depends on the Chebychev polynomial employed to fit to. Thus, if we use
,
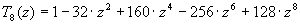or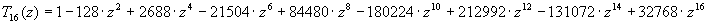 
we have a nine-parameter problem and a
seventeen-parameter problem, respectively. The objective function value
of the optimum is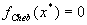 
, i.e.,
the solution and the Chebychev polynomial fit exactly.
Related Papers:
[ALN03] E. Alba, F. Luna, and A.J. Nebro.Parallel Heterogenous Genetic Algorithms for Continuous Optimization. NIDISC'03 (to appear), 2003.
[HL00] F. Herrera and M. Lozano. Gradual Distributed Real-Coded Genetic Algorithms. IEEE Transactions on Evolutionary Computation, 4(1): 43-63, 2000.
[RG75] L.R. Rabiner and B. Gold. Theory and Applications of Digital Signal Processing. Prentice-Hall, Englewood Cliffs, N.J.,1975.
[SP95] R. Storn and K. Price. Differential evolution - A simple efficient adaptive scheme for global optimization over continuous spaces. Technical Report 95-012, Int. Comp. Sci. Inst., Berkeley, CA, 1995.
Click here to get the bibliography in bibtex format.
Last Updated:
4/7/03
For any question or suggestion, click here
to contact with us.