The Edge 2-Connectivity Augmentation Problem

Description:

The E2-AUG problem is a classified NP-hard optimization problem. It can be defined as:

Input:
-Undirected and conected graph G=(V,E).
-Disjoint set A of weighted edges between nodes in V.

Output:
-A subset S A of edges such that G=(V,ES) is edge-biconnected.

Question

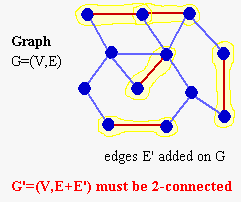
The edge-biconnectivity augmentation problem, wich is sometimes also called bridge-connectivity augmentation problem, can be stated as follows: an undirected, connected graph G=(V,E), with node set V and edge-set E, and an additional, disjoint set A of edges between nodes in V are given. Each edge e A has associated cost c(e)>0 and can be used to augment graph G.

The objective is to identify a subset S A of edges with minimum total costs _{e in S} c(e) such that the augmented graph G = (V,ES) is edge biconnected.

In the design of communication networks, robustness against failure is an important issue. Redundant communication routes are often introduced in order to ensure that any two nodes do not loose connection in case of a single failure in a link or relaying node. An undirected graph that might represent a communication network is said to be edge-biconnected if at least two edges need to be removed in order to separate the graph into disconnected components. In a graph that is not edge-biconnected, a crticial edge whose removal would disconnect the graph is called uncovered edge or bridge.

Problem Instances

In order to define an instance of this problem we need to provide all the information about the Graph. This means: his Vertex Set and the associated Edge Set between pairs of vertexs. The edges are weighted, so we have to indicate this value for each one.

Related Bibliography and Papers