The Computer Game Path Finding Problem

Description:
The Computer Game Path Finding Problem is a path finding optimization problem to be solved in a game computer dynamic (changeable) environment.
Background:
This problem is very common in computer games such as first-person shooter games and strategy games in which the world (i.e., the scenario conditions) dynamically changes. It deals mainly with the provision of intelligence to opponents. Artificial intelligent opponents in commercial computer-games are almost exclusively controlled by programmed scripts that contain "holes" allowing the human player to take advantages of it by means of the experience. Fortunately, artificial intelligence techniques are being applied to provide "human" intelligence to opponents what makes more attractive the game. Moreover, evolutionary learning techniques have already being partially applied to generate intelligent opponents and have been shown to be more effective than script-controlled opponents. The Computer Game Path Finding Problem is adequate to continue doing research in this line.
Characters:
The problem involves several characters:
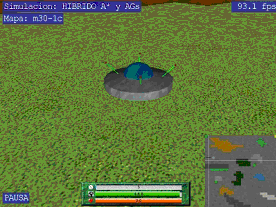
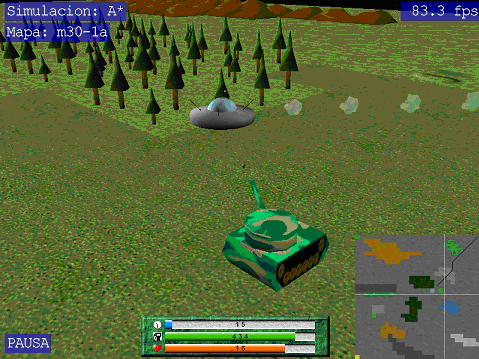
- A main vehicle that can move around the world (see below) and has associated a set of finite resources (time, strength and combustible) whose expenditure has to minimize. In the Figure, the bars in the bottom represent the amount of resources associated to the vehicle..
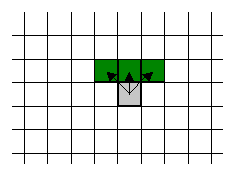
The vehicle is in possesion of three sensors, positioned in its front-head, that can detect the presence of enemies (see Figure below) as well as the nature of the terrain (see also world definition).
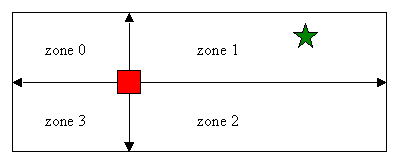
The vehicle can also rotate 45º to change its moving direction. It also owns a goal sensor that allows to detect the zone in which the final position to reach is as it is shown in the Figure below where the vehicle position is represented by a red square whereas the green star represents the position of the goal.
- A set of enemies that try to defeat the main vehicle by shooting it. Each time the main vehicle receives an impact as consequence of the shooting of an enemy, its strength is reduced (besides the vehicle inmmediately is destroyed if it collides with an enemy). Below we show a possible enemy in a game simulation.

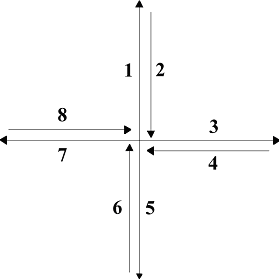
There are two kinds of enemies, static and dynamic. The first ones remain fixed in a position of the world whereas the second ones patrol by following the sequence: North-East-South-West as shown in the Figure below. These patrols are cyclic.
- A non-toroidal world (i.e. with closed frontiers that cannot
be traversed) that is divided in adjacent cells each of which represents
a non-homogeneous piece of terrain. There exist different classes of
terrain and each of them is associated with a different cost (i.e.,
time/combustible units) to be traversed by the vehicle (see below).
The classes of terrain are: free, pool, gravel, bush, tree, hill,
mountain and water. Some of these are traversable and another
are non-traversable. Each time the vehicle traverses a piece of terrain
its combustible and/or its associated time is reduced in a numberof
untis according to the kind of terrain.
The world is also divided in four zones relative to the position of the vehicle as shown in the Figure above about the goal sensor.
There are also three classes of worlds depending on the kind of enemies coexisting in it: static, dynamic or mixed (i.e., combining static and dynamic enemies). The most interestng instances of these problems are those involving dynamic worlds as these are the most popular in computer games.
Question
The problem consists of finding the optimal path that allows the main vehicle, initially positioned in coordinates (xo,yo), arrives safely to a final position (xf,yf). By safely we mean that its associated resources are not exhausted. By optimal we mean that its resources are optimized in the following way: maximize both strengths and combustible, and minimize time spend in move along a solution path.
Problem Instances
We have managed 60 different instances of this problem. Please, contact afdez@lcc.uma.es for more information about it.
Simulation Examples
Below we present some examples of difefrent states that were employed to show the solving of this problem in game-based simulations.different worls. In the first Figure the main vehicle is under the attack of one dynamic enemy that tries to defeat it. The reader can observe the bars in the bottom of the window that provide information about the resources consumed util that moment of the simulation (i.e., until the vehicle has traversed part of the path to go to the final position, if this is ever reached), and a small global map in the right-bottom corner that visualizes the global world where different colours represent different terrains, and the position of the vehicle is also indicated. In the second Figure, the vehicle reaches safely the goal position before being defeating by enemies.

Related Bibliography and Papers
|
TextBook
|
Game Programming Gems by DeLoura, Mark, editor Editorial Charles River Media, INC, 2000 |
|
Journal Paper
|
Artificial Player for Quake III Arena by Van Waveren J. M. P. and L. J. M. Rothkrantz International Journal of Intelligent Games & Simulation, vol.1(1):25-32, 2003 |
|
Journal Paper
|
Improving Opponent Intellignece through Offline Evolutionary Learning by Spronck Pieter, Sprinkhuizen-Kuyper Ida and Postma Eric. International Journal of Intelligent Games & Simulation, vol.2(1):20-27, February 2003 |
| Conference Paper |
Using a Hybrid Evolutionary-A* Approach for Learning Reactive Behaviours. by Cotta Carlos and Troya José M.S. Cagnoni et al. (editores.) LNCS 1803. pps: 347-356, Springer-Verlag, Berlin, 2000 |
| Conference Paper |
Experiencias Evolutivas en Mundos dinámicos de un VideoJuego con Pathfinding Antonio J. Fernández and Javier Jiménez González Aceptado en MAEB'04 |
| URL |
An optimal pathfinder for vehicles in real-world digital terrain maps. by Markus Jönsson, F |
|
URL
|
A compendium of NP optimization problems http://www.nada.kth.se/~viggo/problemlist/compendium.html |