The Minimum Graph Bisection Problem

Description:

The Bisection problem is a classified NP-hard optimization problem. It can be defined as:

Input:
-Undirected and unweighted graph G=(V,E).

Output:
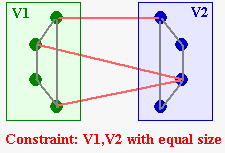
-A partition of V into disjoint sets {V1,V2} with the same size.

Question

A bisection of a graph G=(V,E) with an even number of vertices is a pair of disjoint subsets V1,V2 V of equal size. The cost of a bisection is the number of edges c=(a,b) E such that a V1 and b V2. The problem of Graph Bisection takes as input a graph with an even number of vertices and returns a bisection of minimum cost.

This problem arises frequently in real world applications, such as parallel scientific computing, VLSI design, or task scheduling.

Problem Instances

In order to define an instance of this problem we need to provide all the information about the Graph. This means: his Vertex Set and the associated Edge Set between pairs of vertexs. The edges are unweighted.

Related Bibliography and Papers

Last Updated: 5/06/03                                                                                                                  For any question or suggestion, click here to contact with us.